XGBOOST 调参

发表于 | 分类于

XGBOOST的参数

1.  通用参数：宏观函数控制。
2.  Booster参数：控制每一步的booster(tree/regression)。
3.  学习目标参数：控制训练目标的表现。

通用参数

  1. booster[默认gbtree]

    • 选择每次迭代的模型，有两种选择：
    • gbtree：基于树的模型
    • gbliner：线性模型

  2. silent[默认0]

    • 当这个参数值为1时，静默模式开启，不会输出任何信息。 一般这个参数就保持默认的0，因为这样能帮我们更好地理解模型。

  3. nthread[默认值为最大可能的线程数]

    • 这个参数用来进行多线程控制，应当输入系统的核数。 如果你希望使用CPU全部的核，那就不要输入这个参数，算法会自动检测它。
    • 还有两个参数，XGBoost会自动设置，目前你不用管它。接下来咱们一起看booster参数。

booster参数

尽管有两种booster可供选择，我这里只介绍tree booster，因为它的表现远远胜过linear booster，所以linear booster很少用到。

  1. eta[默认0.3]

    • 和GBM中的 learning rate 参数类似。 通过减少每一步的权重，可以提高模型的鲁棒性。 典型值为0.01-0.2。

  2. min_child_weight[默认1]

    • 决定最小叶子节点样本权重和。 和GBM的 min_child_leaf 参数类似，但不完全一样。XGBoost的这个参数是最小样本权重的和，而GBM参数是最小样本总数。 这个参数用于避免过拟合。当它的值较大时，可以避免模型学习到局部的特殊样本。 但是如果这个值过高，会导致欠拟合。这个参数需要使用CV来调整。

  3. max_depth[默认6]

    • 和GBM中的参数相同，这个值为树的最大深度。 这个值也是用来避免过拟合的。max_depth越大，模型会学到更具体更局部的样本。 需要使用CV函数来进行调优。 典型值：3-10

  4. max_leaf_nodes

    • 树上最大的节点或叶子的数量。 可以替代max_depth的作用。因为如果生成的是二叉树，一个深度为n的树最多生成n2个叶子。 如果定义了这个参数，GBM会忽略max_depth参数。

  5. gamma[默认0]

    • 在节点分裂时，只有分裂后损失函数的值下降了，才会分裂这个节点。Gamma指定了节点分裂所需的最小损失函数下降值。 这个参数的值越大，算法越保守。这个参数的值和损失函数息息相关，所以是需要调整的。

  6. max_delta_step[默认0]

    • 这参数限制每棵树权重改变的最大步长。如果这个参数的值为0，那就意味着没有约束。如果它被赋予了某个正值，那么它会让这个算法更加保守。 通常，这个参数不需要设置。但是当各类别的样本十分不平衡时，它对逻辑回归是很有帮助的。 这个参数一般用不到，但是你可以挖掘出来它更多的用处。

  7. subsample[默认1]

    • 和GBM中的subsample参数一模一样。这个参数控制对于每棵树，随机采样的比例。 减小这个参数的值，算法会更加保守，避免过拟合。但是，如果这个值设置得过小，它可能会导致欠拟合。 典型值：0.5-1

  8. colsample_bytree[默认1]

    • 和GBM里面的max_features参数类似。用来控制每棵随机采样的列数的占比(每一列是一个特征)。 典型值：0.5-1

  9. colsample_bylevel[默认1]

    • 用来控制树的每一级的每一次分裂，对列数的采样的占比。 我个人一般不太用这个参数，因为subsample参数和colsample_bytree参数可以起到相同的作用。但是如果感兴趣，可以挖掘这个参数更多的用处。

  10. lambda[默认1]

    • 权重的L2正则化项。(和Ridge regression类似)。 这个参数是用来控制XGBoost的正则化部分的。虽然大部分数据科学家很少用到这个参数，但是这个参数在减少过拟合上还是可以挖掘出更多用处的。

  11. alpha[默认1]

    • 权重的L1正则化项。(和Lasso regression类似)。 可以应用在很高维度的情况下，使得算法的速度更快。

  12. cale_pos_weight[默认1]

    • 在各类别样本十分不平衡时，把这个参数设定为一个正值，可以使算法更快收敛。

学习目标参数

这个参数用来控制理想的优化目标和每一步结果的度量方法。

  1. objective[默认reg:linear]

    • 这个参数定义需要被最小化的损失函数。最常用的值有：
      • binary:logistic 二分类的逻辑回归，返回预测的概率(不是类别)。
      • multi:softmax 使用softmax的多分类器，返回预测的类别(不是概率)。
        • 在这种情况下，你还需要多设一个参数：num_class(类别数目)。
      • multi:softprob 和multi:softmax参数一样，但是返回的是每个数据属于各个类别的概率。

  2. eval_metric[默认值取决于objective参数的取值]

    • 对于有效数据的度量方法。
    • 对于回归问题，默认值是rmse，对于分类问题，默认值是error。
    • 典型值有：
      • rmse 均方根误差\((\sqrt{\frac{\sum_{i=1}^{N}\epsilon^{2}}{N}})\)
      • mae 平均绝对误差\((\frac{\sum_{i=1}^{N}\left | \epsilon \right |}{N})\)
      • logloss 负对数似然函数值
      • error 二分类错误率(阈值为0.5)
      • merror 多分类错误率
      • mlogloss 多分类
      • logloss损失函数
      • auc 曲线下面积

  3. seed(默认0)

    • 随机数的种子 设置它可以复现随机数据的结果，也可以用于调整参数

如果你之前用的是Scikit-learn,你可能不太熟悉这些参数。但是有个好消息，python的XGBoost模块有一个sklearn包，XGBClassifier。这个包中的参数是按sklearn风格命名的。会改变的函数名是： 1. #### eta ->learning_rate 2. #### lambda->reg_lambda 3. #### alpha->reg_alpha

你肯定在疑惑为啥咱们没有介绍和GBM中的’n_estimators’类似的参数。XGBClassifier中确实有一个类似的参数，但是，是在标准XGBoost实现中调用拟合函数时，把它作为’num_boosting_rounds’参数传入。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#Import libraries:
import pandas as pd
import numpy as np
import xgboost as xgb
from xgboost.sklearn import XGBClassifier
from sklearn import cross_validation, metrics   #Additional scklearn functions
from sklearn.grid_search import GridSearchCV   #Perforing grid search
import matplotlib.pylab as plt
%matplotlib inline
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 12, 4
train = pd.read_csv('train_modified_xgb.csv')
target = 'Disbursed'
IDcol = 'ID'

注意我import了两种XGBoost：

  • xgb - 直接引用xgboost。接下来会用到其中的“cv”函数。
  • XGBClassifier - 是xgboost的sklearn包。这个包允许我们像GBM一样使用Grid Search 和并行处理。

在向下进行之前，我们先定义一个函数，它可以帮助我们建立XGBoost models 并进行交叉验证。好消息是你可以直接用下面的函数，以后再自己的models中也可以使用它。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def modelfit(alg, dtrain, predictors,useTrainCV=True, cv_folds=5, early_stopping_rounds=50):
    
    if useTrainCV:
        xgb_param = alg.get_xgb_params()
        xgtrain = xgb.DMatrix(dtrain[predictors].values, label=dtrain[target].values)
        cvresult = xgb.cv(xgb_param, xgtrain, num_boost_round=alg.get_params()['n_estimators'],show_stdv=False, nfold=cv_folds,metrics='auc', early_stopping_rounds=early_stopping_rounds)
        alg.set_params(n_estimators=cvresult.shape[0])
    
    #Fit the algorithm on the data
    alg.fit(dtrain[predictors], dtrain['Disbursed'],eval_metric='auc')
        
    #Predict training set:
    dtrain_predictions = alg.predict(dtrain[predictors])
    dtrain_predprob = alg.predict_proba(dtrain[predictors])[:,1]
        
    #Print model report:
    print "\nModel Report"
    print "Accuracy : %.4g" % metrics.accuracy_score(dtrain['Disbursed'].values, dtrain_predictions)
    print "AUC Score (Train): %f" % metrics.roc_auc_score(dtrain['Disbursed'], dtrain_predprob)
                    
    feat_imp = pd.Series(alg.booster().get_fscore()).sort_values(ascending=False)
    feat_imp.plot(kind='bar', title='Feature Importances')
    plt.ylabel('Feature Importance Score')

这个函数和GBM中使用的有些许不同。不过本文章的重点是讲解重要的概念，而不是写代码。如果哪里有不理解的地方，请在下面评论，不要有压力。注意xgboost的sklearn包没有“feature_importance”这个量度，但是get_fscore()函数有相同的功能。

参数调优的一般方法

我们会使用和GBM中相似的方法。需要进行如下步骤：

  1. 选择较高的学习速率(learning rate)。一般情况下，学习速率的值为0.1。但是，对于不同的问题，理想的学习速率有时候会在0.05到0.3之间波动。选择对应于此学习速率的理想决策树数量。XGBoost有一个很有用的函数“cv”，这个函数可以在每一次迭代中使用交叉验证，并返回理想的决策树数量。

  2. 对于给定的学习速率和决策树数量，进行决策树特定参数调优(max_depth, min_child_weight, gamma, subsample, colsample_bytree)。在确定一棵树的过程中，我们可以选择不同的参数，待会儿我会举例说明。

  3. xgboost的正则化参数的调优。(lambda, alpha)。这些参数可以降低模型的复杂度，从而提高模型的表现。

  4. 降低学习速率，确定理想参数。

咱们一起详细地一步步进行这些操作。

第一步：确定学习速率和tree_based 参数调优的估计器数目

为了确定boosting参数，我们要先给其它参数一个初始值。咱们先按如下方法取值：

  1. max_depth = 5 :这个参数的取值最好在3-10之间。我选的起始值为5，但是你也可以选择其它的值。起始值在4-6之间都是不错的选择。

  2. min_child_weight = 1:在这里选了一个比较小的值，因为这是一个极不平衡的分类问题。因此，某些叶子节点下的值会比较小。

  3. gamma = 0: 起始值也可以选其它比较小的值，在0.1到0.2之间就可以。这个参数后继也是要调整的。

  4. subsample, colsample_bytree = 0.8: 这个是最常见的初始值了。典型值的范围在0.5-0.9之间。

  5. scale_pos_weight = 1: 这个值是因为类别十分不平衡。 注意哦，上面这些参数的值只是一个初始的估计值，后继需要调优。这里把学习速率就设成默认的0.1。然后用xgboost中的cv函数来确定最佳的决策树数量。前文中的函数可以完成这个工作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#Choose all predictors except target & IDcols
predictors = [x for x in train.columns if x not in [target, IDcol]]
xgb1 = XGBClassifier(
 learning_rate =0.1,
 n_estimators=1000,
 max_depth=5,
 min_child_weight=1,
 gamma=0,
 subsample=0.8,
 colsample_bytree=0.8,
 objective= 'binary:logistic',
 nthread=4,
 scale_pos_weight=1,
 seed=27)
modelfit(xgb1, train, predictors)
Model Report
Accuracy : 0.9854
AUC Score (Train): 0.891681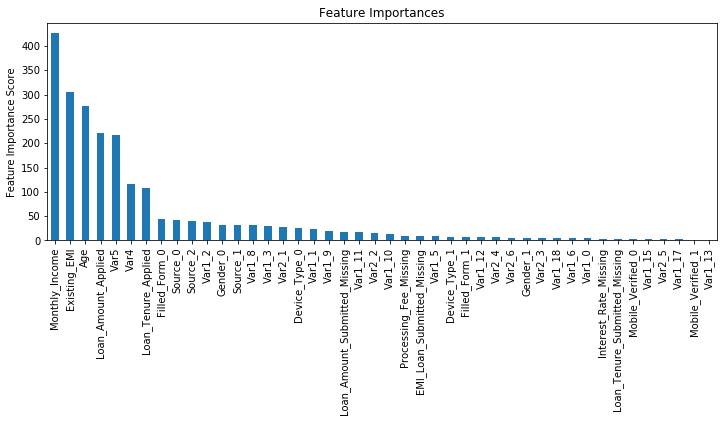
png

png

从输出结果可以看出，在学习速率为0.1时，理想的决策树数目是140。这个数字对你而言可能比较高，当然这也取决于你的系统的性能。

第二步： max_depth 和 min_weight 参数调优

我们先对这两个参数调优，是因为它们对最终结果有很大的影响。首先，我们先大范围地粗调参数，然后再小范围地微调。

注意：在这一节我会进行高负荷的栅格搜索(grid search)，这个过程大约需要15-30分钟甚至更久，具体取决于你系统的性能。你也可以根据自己系统的性能选择不同的值。

1
2
3
4
5
6
7
8
9
10
param_test1 = {
 'max_depth':range(3,10,2),
 'min_child_weight':range(1,6,2)
}
gsearch1 = GridSearchCV(estimator = XGBClassifier(         learning_rate =0.1, n_estimators=140, max_depth=5,
min_child_weight=1, gamma=0, subsample=0.8,             colsample_bytree=0.8,
 objective= 'binary:logistic', nthread=4,     scale_pos_weight=1, seed=27), 
 param_grid = param_test1,     scoring='roc_auc',n_jobs=4,iid=False, cv=5)
gsearch1.fit(train[predictors],train[target])
gsearch1.grid_scores_, gsearch1.best_params_,     gsearch1.best_score_
([mean: 0.83764, std: 0.00875, params: {'max_depth': 3, 'min_child_weight': 1},
  mean: 0.83837, std: 0.00825, params: {'max_depth': 3, 'min_child_weight': 3},
  mean: 0.83716, std: 0.00818, params: {'max_depth': 3, 'min_child_weight': 5},
  mean: 0.84016, std: 0.00680, params: {'max_depth': 5, 'min_child_weight': 1},
  mean: 0.83965, std: 0.00537, params: {'max_depth': 5, 'min_child_weight': 3},
  mean: 0.83935, std: 0.00548, params: {'max_depth': 5, 'min_child_weight': 5},
  mean: 0.83570, std: 0.00587, params: {'max_depth': 7, 'min_child_weight': 1},
  mean: 0.83448, std: 0.00726, params: {'max_depth': 7, 'min_child_weight': 3},
  mean: 0.83456, std: 0.00554, params: {'max_depth': 7, 'min_child_weight': 5},
  mean: 0.82851, std: 0.00651, params: {'max_depth': 9, 'min_child_weight': 1},
  mean: 0.82955, std: 0.00580, params: {'max_depth': 9, 'min_child_weight': 3},
  mean: 0.83158, std: 0.00677, params: {'max_depth': 9, 'min_child_weight': 5}],
 {'max_depth': 5, 'min_child_weight': 1},
 0.8401574515811714)

至此，我们对于数值进行了较大跨度的12中不同的排列组合，可以看出理想的max_depth值为5，理想的min_child_weight值为5。在这个值附近我们可以再进一步调整，来找出理想值。我们把上下范围各拓展1，因为之前我们进行组合的时候，参数调整的步长是2。

1
2
3
4
5
6
7
8
9
10
param_test2 = {
 'max_depth':[4,5,6],
 'min_child_weight':[4,5,6]
}
gsearch2 = GridSearchCV(estimator = XGBClassifier(     learning_rate=0.1, n_estimators=140, max_depth=5,
 min_child_weight=2, gamma=0, subsample=0.8, colsample_bytree=0.8,
 objective= 'binary:logistic', nthread=4, scale_pos_weight=1,seed=27), 
 param_grid = param_test2, scoring='roc_auc',n_jobs=4,iid=False, cv=5)
gsearch2.fit(train[predictors],train[target])
gsearch2.grid_scores_, gsearch2.best_params_,     gsearch2.best_score_
([mean: 0.84034, std: 0.00601, params: {'max_depth': 4, 'min_child_weight': 4},
  mean: 0.83921, std: 0.00658, params: {'max_depth': 4, 'min_child_weight': 5},
  mean: 0.84003, std: 0.00622, params: {'max_depth': 4, 'min_child_weight': 6},
  mean: 0.84071, std: 0.00553, params: {'max_depth': 5, 'min_child_weight': 4},
  mean: 0.83935, std: 0.00548, params: {'max_depth': 5, 'min_child_weight': 5},
  mean: 0.83871, std: 0.00492, params: {'max_depth': 5, 'min_child_weight': 6},
  mean: 0.83926, std: 0.00302, params: {'max_depth': 6, 'min_child_weight': 4},
  mean: 0.83717, std: 0.00483, params: {'max_depth': 6, 'min_child_weight': 5},
  mean: 0.83732, std: 0.00601, params: {'max_depth': 6, 'min_child_weight': 6}],
 {'max_depth': 5, 'min_child_weight': 4},
 0.8407073731353547)

至此，我们得到max_depth的理想取值为4，min_child_weight的理想取值为6。同时，我们还能看到cv的得分有了小小一点提高。需要注意的一点是，随着模型表现的提升，进一步提升的难度是指数级上升的，尤其是你的表现已经接近完美的时候。当然啦，你会发现，虽然min_child_weight的理想取值是6，但是我们还没尝试过大于6的取值。像下面这样，就可以尝试其它值。

1
2
3
4
5
6
7
8
9
10
11
param_test2b = {
 'min_child_weight':[6,8,10,12]
 }
gsearch2b = GridSearchCV(estimator = XGBClassifier(     learning_rate=0.1, n_estimators=140, max_depth=4,
 min_child_weight=2, gamma=0, subsample=0.8, colsample_bytree=0.8, objective= 'binary:logistic', nthread=4, scale_pos_weight=1,seed=27), param_grid = param_test2b, scoring='roc_auc',n_jobs=4,iid=False, cv=5)
gsearch2b.fit(train[predictors],train[target])
modelfit(gsearch2b.best_estimator_, train, predictors)
gsearch2b.grid_scores_, gsearch2b.best_params_, gsearch2b.best_score_
Model Report
Accuracy : 0.9854
AUC Score (Train): 0.875086





([mean: 0.84003, std: 0.00622, params: {'min_child_weight': 6},
  mean: 0.83889, std: 0.00714, params: {'min_child_weight': 8},
  mean: 0.84004, std: 0.00661, params: {'min_child_weight': 10},
  mean: 0.83869, std: 0.00632, params: {'min_child_weight': 12}],
 {'min_child_weight': 10},
 0.840037896893036)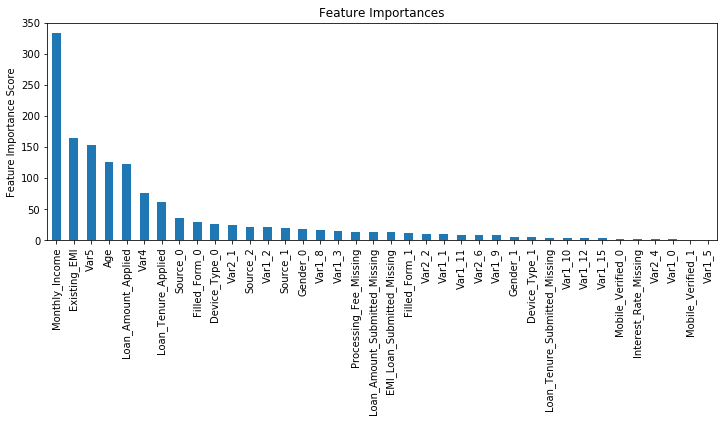
png

png

我们可以看出，6确确实实是理想的取值了。

第三步：gamma参数调优

在已经调整好其它参数的基础上，我们可以进行gamma参数的调优了。Gamma参数取值范围可以很大，我这里把取值范围设置为5了。你其实也可以取更精确的gamma值。

1
2
3
4
5
6
7
param_test3 = {
 'gamma':[i/10.0 for i in range(0,5)]
}
gsearch3 = GridSearchCV(estimator = XGBClassifier( learning_rate =0.1, n_estimators=140, max_depth=4, min_child_weight=6, gamma=0, subsample=0.8, colsample_bytree=0.8, objective= 'binary:logistic', nthread=4, scale_pos_weight=1,seed=27), param_grid = param_test3, scoring='roc_auc',n_jobs=4,iid=False, cv=5)
gsearch3.fit(train[predictors],train[target])
gsearch3.grid_scores_, gsearch3.best_params_, gsearch3.best_score_
([mean: 0.84003, std: 0.00622, params: {'gamma': 0.0},
  mean: 0.84017, std: 0.00594, params: {'gamma': 0.1},
  mean: 0.83963, std: 0.00624, params: {'gamma': 0.2},
  mean: 0.83974, std: 0.00692, params: {'gamma': 0.3},
  mean: 0.83996, std: 0.00568, params: {'gamma': 0.4}],
 {'gamma': 0.1},
 0.8401672862430356)

从这里可以看出来，我们在第一步调参时设置的初始gamma值就是比较合适的。也就是说，理想的gamma值为0。在这个过程开始之前，最好重新调整boosting回合，因为参数都有变化。

从这里，可以看出，得分提高了。所以，最终得到的参数是：

1
2
3
4
5
6
7
8
9
10
11
12
13
xgb2 = XGBClassifier(
 learning_rate =0.1,
 n_estimators=1000,
 max_depth=4,
 min_child_weight=6,
 gamma=0,
 subsample=0.8,
 colsample_bytree=0.8,
 objective= 'binary:logistic',
 nthread=4,
scale_pos_weight=1,
seed=27)
modelfit(xgb2, train, predictors)
Model Report
Accuracy : 0.9854
AUC Score (Train): 0.883777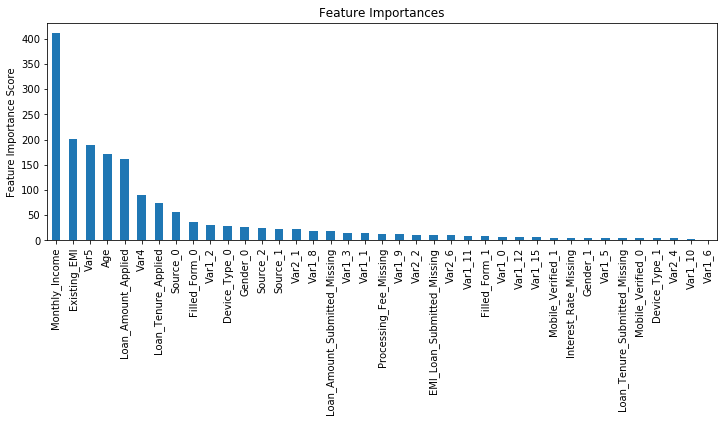
png

png

调整subsample 和 colsample_bytree 参数

下一步是尝试不同的subsample 和 colsample_bytree 参数。我们分两个阶段来进行这个步骤。这两个步骤都取0.6,0.7,0.8,0.9作为起始值。

1
2
3
4
5
6
7
8
9
param_test4 = {
 'subsample':[i/10.0 for i in range(6,10)],
 'colsample_bytree':[i/10.0 for i in range(6,10)]
}
gsearch4 = GridSearchCV(estimator = XGBClassifier( learning_rate =0.1, n_estimators=177, max_depth=3, min_child_weight=4, gamma=0.1, subsample=0.8, colsample_bytree=0.8, objective= 'binary:logistic', nthread=4, scale_pos_weight=1,seed=27), param_grid = param_test4, scoring='roc_auc',n_jobs=4,iid=False, cv=5)
gsearch4.fit(train[predictors],train[target])
gsearch4.grid_scores_, gsearch4.best_params_, gsearch4.best_score_
([mean: 0.83836, std: 0.00840, params: {'subsample': 0.6, 'colsample_bytree': 0.6},
  mean: 0.83720, std: 0.00976, params: {'subsample': 0.7, 'colsample_bytree': 0.6},
  mean: 0.83787, std: 0.00758, params: {'subsample': 0.8, 'colsample_bytree': 0.6},
  mean: 0.83776, std: 0.00762, params: {'subsample': 0.9, 'colsample_bytree': 0.6},
  mean: 0.83923, std: 0.01005, params: {'subsample': 0.6, 'colsample_bytree': 0.7},
  mean: 0.83800, std: 0.00853, params: {'subsample': 0.7, 'colsample_bytree': 0.7},
  mean: 0.83819, std: 0.00779, params: {'subsample': 0.8, 'colsample_bytree': 0.7},
  mean: 0.83925, std: 0.00906, params: {'subsample': 0.9, 'colsample_bytree': 0.7},
  mean: 0.83977, std: 0.00831, params: {'subsample': 0.6, 'colsample_bytree': 0.8},
  mean: 0.83867, std: 0.00870, params: {'subsample': 0.7, 'colsample_bytree': 0.8},
  mean: 0.83879, std: 0.00797, params: {'subsample': 0.8, 'colsample_bytree': 0.8},
  mean: 0.84144, std: 0.00854, params: {'subsample': 0.9, 'colsample_bytree': 0.8},
  mean: 0.83878, std: 0.00760, params: {'subsample': 0.6, 'colsample_bytree': 0.9},
  mean: 0.83922, std: 0.00823, params: {'subsample': 0.7, 'colsample_bytree': 0.9},
  mean: 0.83912, std: 0.00765, params: {'subsample': 0.8, 'colsample_bytree': 0.9},
  mean: 0.83926, std: 0.00843, params: {'subsample': 0.9, 'colsample_bytree': 0.9}],
 {'colsample_bytree': 0.8, 'subsample': 0.9},
 0.8414372201469303)

从这里可以看出来，subsample 和 colsample_bytree 参数的理想取值都是0.8。现在，我们以0.05为步长，在这个值附近尝试取值。

1
2
3
4
5
6
7
8
9
10
param_test5 = {
 'subsample':[i/100.0 for i in range(75,90,5)],
 'colsample_bytree':[i/100.0 for i in range(75,90,5)]
}
gsearch5 = GridSearchCV(estimator = XGBClassifier( learning_rate =0.1, n_estimators=177, max_depth=4,
 min_child_weight=6, gamma=0, subsample=0.8, colsample_bytree=0.8,
 objective= 'binary:logistic', nthread=4, scale_pos_weight=1,seed=27), 
 param_grid = param_test5, scoring='roc_auc',n_jobs=4,iid=False, cv=5)
gsearch5.fit(train[predictors],train[target])
gsearch5.grid_scores_, gsearch4.best_params_, gsearch4.best_score_
([mean: 0.83922, std: 0.00800, params: {'subsample': 0.75, 'colsample_bytree': 0.75},
  mean: 0.84068, std: 0.00664, params: {'subsample': 0.8, 'colsample_bytree': 0.75},
  mean: 0.84012, std: 0.00744, params: {'subsample': 0.85, 'colsample_bytree': 0.75},
  mean: 0.83893, std: 0.00756, params: {'subsample': 0.75, 'colsample_bytree': 0.8},
  mean: 0.84070, std: 0.00665, params: {'subsample': 0.8, 'colsample_bytree': 0.8},
  mean: 0.84030, std: 0.00663, params: {'subsample': 0.85, 'colsample_bytree': 0.8},
  mean: 0.83961, std: 0.00628, params: {'subsample': 0.75, 'colsample_bytree': 0.85},
  mean: 0.83964, std: 0.00494, params: {'subsample': 0.8, 'colsample_bytree': 0.85},
  mean: 0.84064, std: 0.00733, params: {'subsample': 0.85, 'colsample_bytree': 0.85}],
 {'colsample_bytree': 0.8, 'subsample': 0.9},
 0.8414372201469303)

我们得到的理想取值还是原来的值。因此，最终的理想取值是:

  • subsample: 0.8
  • colsample_bytree: 0.8

第五步：正则化参数调优

下一步是应用正则化来降低过拟合。由于gamma函数提供了一种更加有效地降低过拟合的方法，大部分人很少会用到这个参数。但是我们在这里也可以尝试用一下这个参数。我会在这里调整’reg_alpha’参数，然后’reg_lambda’参数留给你来完成。

1
2
3
4
5
6
7
8
9
param_test6 = {
 'reg_alpha':[1e-5, 1e-2, 0.1, 1, 100]
}
gsearch6 = GridSearchCV(estimator = XGBClassifier( learning_rate =0.1, n_estimators=177, max_depth=4,
 min_child_weight=6, gamma=0.1, subsample=0.8, colsample_bytree=0.8,
 objective= 'binary:logistic', nthread=4, scale_pos_weight=1,seed=27), 
 param_grid = param_test6, scoring='roc_auc',n_jobs=4,iid=False, cv=5)
gsearch6.fit(train[predictors],train[target])
gsearch6.grid_scores_, gsearch6.best_params_, gsearch6.best_score_
([mean: 0.83949, std: 0.00720, params: {'reg_alpha': 1e-05},
  mean: 0.83940, std: 0.00607, params: {'reg_alpha': 0.01},
  mean: 0.84005, std: 0.00638, params: {'reg_alpha': 0.1},
  mean: 0.84062, std: 0.00775, params: {'reg_alpha': 1},
  mean: 0.81217, std: 0.01559, params: {'reg_alpha': 100}],
 {'reg_alpha': 1},
 0.8406243437179736)

我们可以看到，相比之前的结果，CV的得分甚至还降低了。但是我们之前使用的取值是十分粗糙的，我们在这里选取一个比较靠近理想值(0.01)的取值，来看看是否有更好的表现。

1
2
3
4
5
6
7
param_test7 = {
 'reg_alpha':[0, 0.001, 0.005, 0.01, 0.05]
}
gsearch7 = GridSearchCV(estimator = XGBClassifier( learning_rate =0.1, n_estimators=177, max_depth=4, min_child_weight=6, gamma=0.1, subsample=0.8, colsample_bytree=0.8, objective= 'binary:logistic', nthread=4, scale_pos_weight=1,seed=27), param_grid = param_test7, scoring='roc_auc',n_jobs=4,iid=False, cv=5)
gsearch7.fit(train[predictors],train[target])
gsearch7.grid_scores_, gsearch7.best_params_, gsearch7.best_score_
([mean: 0.83949, std: 0.00720, params: {'reg_alpha': 0},
  mean: 0.83949, std: 0.00720, params: {'reg_alpha': 0.001},
  mean: 0.83999, std: 0.00658, params: {'reg_alpha': 0.005},
  mean: 0.83940, std: 0.00607, params: {'reg_alpha': 0.01},
  mean: 0.83945, std: 0.00693, params: {'reg_alpha': 0.05}],
 {'reg_alpha': 0.005},
 0.8399870466856136)

可以看到，CV的得分提高了。现在，我们在模型中来使用正则化参数，来看看这个参数的影响。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
xgb3 = XGBClassifier(
 learning_rate =0.1,
 n_estimators=1000,
 max_depth=4,
 min_child_weight=6,
 gamma=0,
 subsample=0.8,
 colsample_bytree=0.8,
 reg_alpha=0.005,
 objective= 'binary:logistic',
 nthread=4,
 scale_pos_weight=1,
 seed=27)
modelfit(xgb3, train, predictors)
Model Report
Accuracy : 0.9854
AUC Score (Train): 0.883621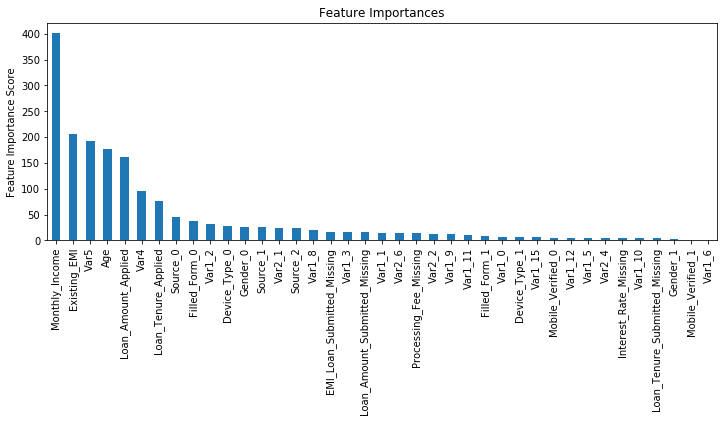
png

png

然后我们发现性能有了小幅度提高。

第6步：降低学习速率

最后，我们使用较低的学习速率，以及使用更多的决策树。我们可以用XGBoost中的CV函数来进行这一步工作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
xgb4 = XGBClassifier(
 learning_rate =0.01,
 n_estimators=5000,
 max_depth=4,
 min_child_weight=6,
 gamma=0,
 subsample=0.8,
 colsample_bytree=0.8,
 reg_alpha=0.005,
 objective= 'binary:logistic',
 nthread=4,
 scale_pos_weight=1,
 seed=27)
modelfit(xgb4, train, predictors)
Model Report
Accuracy : 0.9854
AUC Score (Train): 0.884030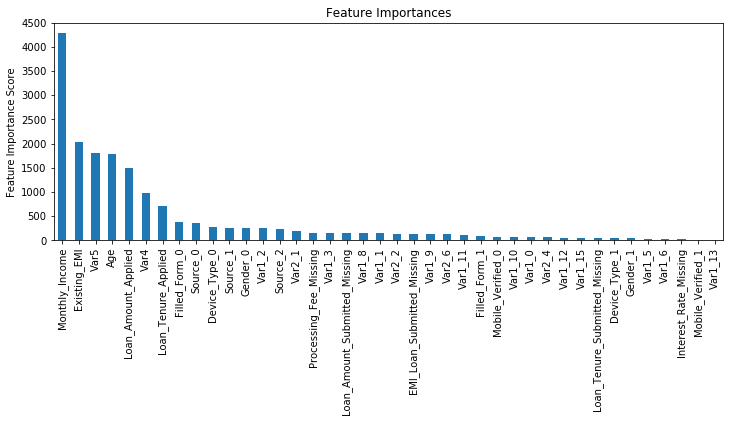
png

png

至此，你可以看到模型的表现有了大幅提升，调整每个参数带来的影响也更加清楚了。 在文章的末尾，我想分享两个重要的思想： 1. 仅仅靠参数的调整和模型的小幅优化，想要让模型的表现有个大幅度提升是不可能的。GBM的最高得分是0.8487，XGBoost的最高得分是0.8494。确实是有一定的提升，但是没有达到质的飞跃。 2. 要想让模型的表现有一个质的飞跃，需要依靠其他的手段，诸如，特征工程(feature egineering) ，模型组合(ensemble of model),以及堆叠(stacking)等。

1
2